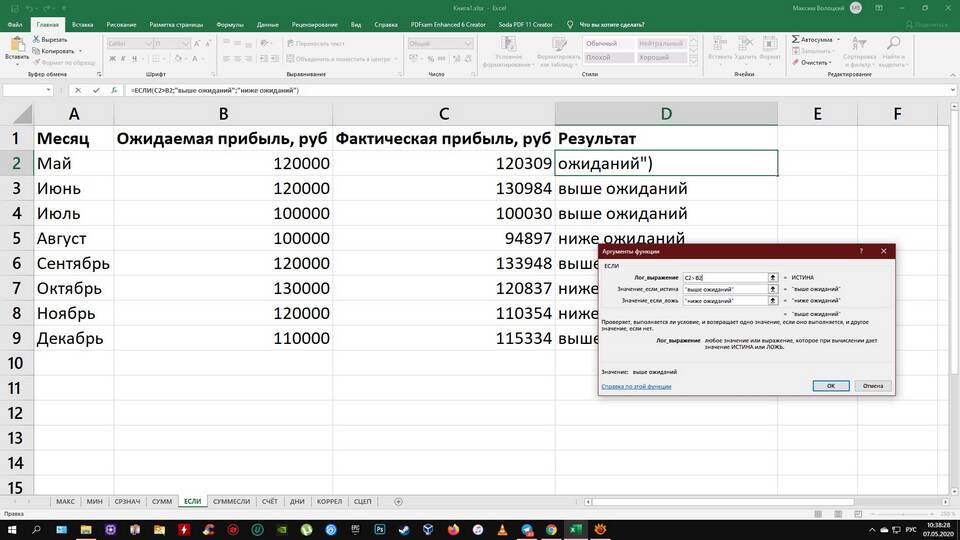
Формулы представляют собой математические выражения, используемые для вычислений и анализа данных. Рассмотрим основные элементы, которые могут входить в состав формул в различных областях применения.
Содержание
Базовые компоненты формул
| Элемент | Примеры | Применение |
| Числовые константы | 5, 3.14, -2.5 | Базовые значения для расчетов |
| Переменные | x, y, a, b | Обозначение неизвестных величин |
| Математические операторы | +, -, *, /, ^ | Арифметические операции |
Математические функции в формулах
Основные функции
- Тригонометрические: sin, cos, tan
- Логарифмические: log, ln
- Экспоненциальные: exp
- Статистические: среднее, медиана
- Финансовые: NPV, IRR
Специальные символы и обозначения
- Греческие буквы: α, β, γ
- Скобки: (), [], {}
- Индексы и степени: x², aₙ
- Символы отношений: =, ≠, ≤, ≥
- Логические операторы: ∧, ∨, ¬
Типы данных в формулах
| Тип данных | Использование |
| Целые числа | Дискретные вычисления |
| Дробные числа | Точные расчеты |
| Текстовые строки | Формулы с условиями |
| Логические значения | Условные выражения |
Специфические элементы для разных областей
- Физические константы (скорость света, гравитационная постоянная)
- Химические элементы и соединения (H₂O, CO₂)
- Финансовые показатели (ROI, EBITDA)
- Статистические меры (σ, μ)
- Программные переменные и функции
Правила составления формул
- Соблюдать порядок операций
- Использовать правильные типы данных
- Учитывать область определения функций
- Проверять баланс скобок
- Обеспечивать единообразие обозначений
Заключение
Формулы могут включать широкий спектр элементов - от простых чисел до сложных специализированных функций. Грамотное сочетание этих компонентов позволяет создавать точные и эффективные математические выражения для решения различных задач. Понимание возможностей и ограничений каждого элемента формул является ключом к их правильному составлению и применению.